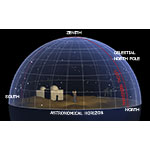
Altazimuth coordinates are one of the three traditional systems of orthogonal spherical reference (i.e., in which each of the two series of circles used to identify the coordinates of a point on the celestial sphere intersect at right angles) employed in positional astronomy.

Unlike the other two systems—equatorial coordinates and ecliptic coordinates—the altazimuth coordinates are a local reference: they are specific to the place of observation, not to the heavenly bodies. Since the positions of the latter generally change with the observer's geographic coordinates, and since the celestial sphere appears to rotate from east to west around the celestial poles in about twenty-four hours, the two position angles of the celestial body in the altazimuth coordinates—altitude (Latin altitudo) and azimuth (from which the system gets its name)—are meaningless unless we also specify the latitude and longitude of the place and the exact hour of the observation.

As the related terminology suggests, altazimuth coordinates were widely diffused in Islamic astronomy from the ninth century onward. They became known in Europe through the many Latin translations of Arab astronomical texts made in Cordoba, Toledo, and Seville between the tenth and twelfth centuries.

The main great circle of reference used in altazimuth coordinates is the astronomical horizon, locus of the intersection between the celestial sphere and the horizontal plane passing through the eye of the observer.

The concept differs from the standard horizon. If, for example, the observer is on an island in the middle of the ocean, the astronomical horizon is not the dividing line between water and sky. Because the Earth is round, that dividing line lies that much farther below the astronomical horizon as the observer is higher above sea level.

The main axis of reference used in altazimuth coordinates is the right line passing through the observer and perpendicular to the astronomical horizon. It intersects the celestial sphere in two points: the zenith (from the Arabic samt, mistakenly read as sanit, in the expression samt al-ra's = the direction on the head), exactly above the observer's head, and the nadir (from the Arabic nazîr = opposite), exactly below the observer's feet.

Each of the circles that can be drawn on the celestial sphere parallel to the astronomical horizon is called an almucantar (from the Arabic al-muqantarât = the arched bridge). As a set, they constitute the parallels of the celestial sphere in the system of altazimuth coordinates, and in fact are also called altitude parallels.

Each of the great circles intersecting the zenith and the nadir is called a vertical circle or altitude circle. As a set, they constitute the meridians of the celestial sphere in the system of altazimuth coordinates.

The vertical circle that touches the horizon at the geographic north and south is called the local meridian. It is important because in twenty-four hours all celestial bodies cross it when they reach their point of maximum elevation on the horizon (culmination). Moreover, the Sun's crossing of the local meridian signals the instant of true noon, which usually does not coincide with the mean noon shown by the clock.

The first of the two altazimuth coordinates is called azimuth (from the Arabic al-sumût = the directions). It is the angle formed with respect to the meridian line (i.e., the north-south direction in the geographic sense) by the intersection between the vertical circle passing through the celestial body and the astronomical horizon.

In antiquity, the azimuth, ranging between 0° and 360°, was measured from the geographic north and moving eastward, whereas today it is customary to measure it from the geographic south and moving westward. The ancient usage endures in surveying, where the azimuth, or position angle, merely indicates the angle separating a given point of the horizon from the geographic north.

In current use, the second of the two altazimuth coordinates is called altitude. Ranging between 0° and 90°, it is the angle at which the observer sees, on the vertical circle intersecting the celestial body, the underlying arc between the body and the astronomical horizon. By definition, the lower the altitude, the closer the celestial body is to the astronomical horizon.

It is important to bear in mind that in antiquity the second coordinate was the complement of "altitude" in the modern sense, and was known as the zenith distance of the celestial body.

Angle between 0° and 90°, complementary to the altitude, that in a given instant separates the generic celestial body from the observer's zenith By definition, the shorter the zenith distance, the higher the celestial body is above the astronomical horizon.

Every celestial body rises on the horizon and continues its ascent until it crosses the observer's local meridian. The meridian altitude is the angle corresponding to the arc of the local meridian bounded by the transit point of the celestial body (culmination) and the astronomical horizon.