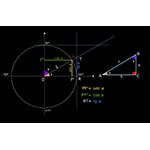
The ratio of two sides of a triangle is a function of its internal angles. In other words, the ratios between any two sides of a triangle are equal to those between the corresponding sides of any triangle similar to it.

Perhaps as early as the 4th century B.C.E, the invariance of these ratios inspired the Greeks to use a special trigonometric relationship. An angle at the center intercepts two points on the circumference; the segment joining them is the angle's chord. The ratio between the chord and the radius of the circumference is determined solely by the angle at the center and, when found, can be tabulated. In his Almagest, Claudius Ptolemy (2nd century C.E.) gives a table of chords, compiled for every half-degree on the basis of a circle with a radius of 60 units. The table provides the chord for a given angle or, vice versa, the angle for a given chord.

By definition, the chord was used in problems where the geometric figures could be decomposed into isosceles triangles. Toward the 6th century E.E., the Indians found it easier to work with right-angled triangles (right triangles) and started using the angle's half-chord. The Islamic astronomer Muhammad al-Battânî (9th century C.E.) described the new relationship as the angle's sine, today expressed by the ratio of the side of the right triangle opposite the angle to the triangle's hypotenuse.

In the 9th century, Islamic scientists developed the two other fundamental trigonometric relationships: the cosine (ratio of the side adjacent the angle and the hypotenuse) and the tangent (ratio of the side opposite the angle to the side adjacent the angle), as well as the respective reciprocal relationships: secant, cosecant and cotangent. For each relationship, they compiled accurate numerical tables to use in solving practical problems.