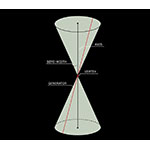
In general, conic sections—or, more succinctly, conics—are the family of curves formed by the intersection of a circular cone with planes at varying angles. The cone is a "double" surface generated by the rotation around a straight line, called axis, of a second straight line, called generator (or generatrix), that intersects the axis in one point (the vertex of the cone) and forms an angle with the axis called the cone's semi-width. The first authors to have described conics and their properties are believed to have been Aristaeus (4th C. B.C.E.) and Euclid (4th-3rd Cs. B.C.E.). Their results, however, soon fell into oblivion, having been overshadowed by the fame of the treatise by Apollonius of Perga (2nd half of 3rd C. B.C.E.) entitled Conics.

When a circular cone intersects a plane perpendicular to its axis, the resulting closed curve is, by definition, a circumference. This special conic is also known as the set of points on the plane equidistant from a given point: the center of the circumference.

If a circular cone intersects a plane whose inclination to the cone's axis is greater than the angle of the generator, the result is a closed curve called an ellipse. The curve tends toward a circumference the more the plane tends toward perpendicularity with the axis; conversely, the curve's elongation increases as the plane's inclination tends toward that of the generator. The ellipse possesses two axes of symmetry perpendicular to each other; their intersection is called the center of the ellipse. Since the two axes correspond to the curve's maximum and minimum widths, they are referred to as the major axis and minor axis respectively. On the major axis, in positions opposite and symmetrical to the center, lie two special points: the foci of the ellipse. The ellipse may be also defined as a geometric locus relative to the foci, namely, as the set of points of the plane whose distances from the foci, when summed, are always equal to a given constant (which exceeds the distance between the foci).

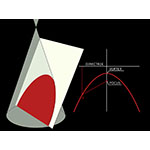
The open curve obtained by intersecting the circular cone with a plane parallel to the generator. The parabola posses a single axis of symmetry, which is therefore called, more simply, the axis of the parabola. The extreme point in which the curve crosses the axis is the vertex of the parabola. Opposite the vertex, and symmetrical to it, are two special points of the axis. The first, in the concave section of the curve, is called the focus of the parabola; the other, lying outside the concave section, marks the shortest distance between the curve and a line perpendicular to the axis, called the directrix of the parabola. The parabola may also be defined as the set of points of the plane equidistant from the focus and the directrix.

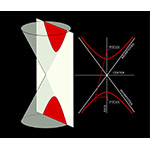
Intersecting the twofold circular cone with a plane inclined to the negative axis of the generator, one obtains on each fold a branch of the curve called a hyperbola. The two branches mirror each other with respect to two perpendicular axes of symmetry, whose intersection is called the center of the hyperbola. On the axis intersecting the hyperbola, and in the concave section of each branch, are two points symmetrical relative to the center: the foci of the hyperbola. The hyperbola can also be defined as the geometric locus of the plane with respect to the foci: it is the set of points the difference of whose distances from the foci is always equal to a given constant (smaller than the distance between the foci). Moving away from the center, the branches of the hyperbola indefinitely approach two straight lines called asymptotes, without ever touching them. Both asymptotes intersect the center of the hyperbole and are symmetrical with respect to the axes.